Butterworth Filter
Overview
This metric applies a the SAE standard Butterworth filter at specified channel frequency classes (CFC). A Butterworth Filter works to filter data and create a steady signal frequency in the range of acceptable signals, specified by the user, while removing any interference in the signals.
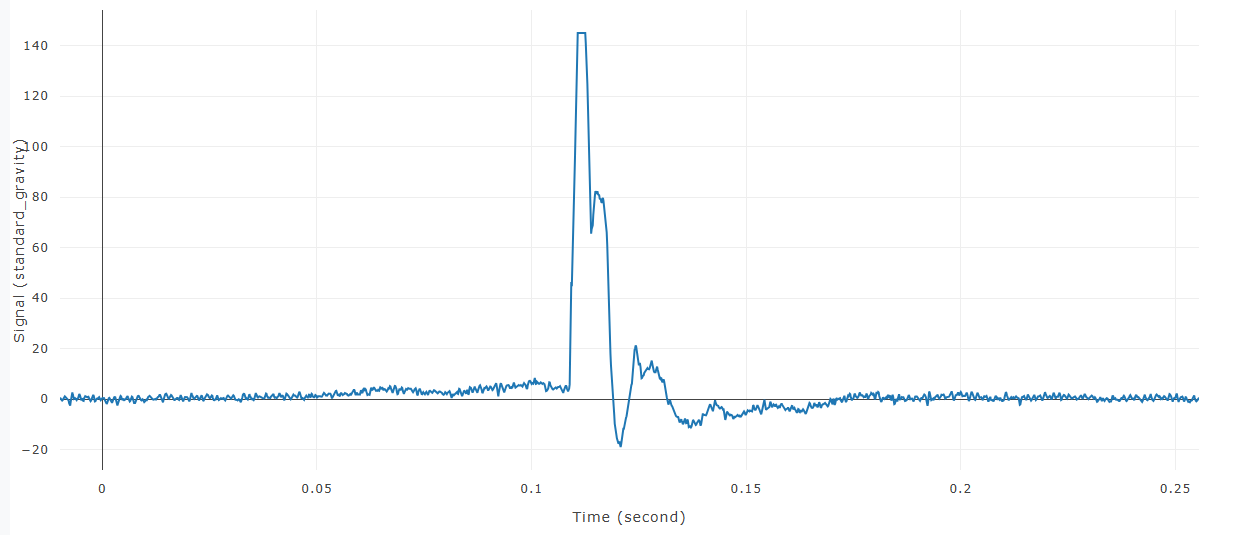
Time History Signal
Select desired CFC for signal:
Calculation
Convert time units to seconds
Calculate sampling rate (T) based on time difference between two consecutive data points
Adds data to the ends of signal if there is not enough padding present
Calculate filter coefficients using selected cutoff frequency and SAE J2111 standards for bandwidth filters
A n g u l a r F r e q u e n c y ( w d ) = 2 p i ∗ f i l t e r c l a s s ∗ 2.0775 Angular\,Frequency\,(wd) = 2pi*filter class*2.0775 A n gu l a r F re q u e n cy ( w d ) = 2 p i ∗ f i lt erc l a ss ∗ 2.0775 N o r m a l i z e d A n g u l a r F r e q u e n c y ( w a ) = s i n ( w d ∗ ( T / 2 ) ) c o s ( w d ∗ ( T / 2 ) ) Normalized\,Angular\,Frequency\,(wa) = \frac{sin(wd*(T/2))}{cos(wd*(T/2))} N or ma l i ze d A n gu l a r F re q u e n cy ( w a ) = cos ( w d ∗ ( T /2 )) s in ( w d ∗ ( T /2 )) D e n o m i n a t o r C o e f f i c i e n t s = { a 0 = w a 2 1 + ( 2 ) ∗ w a + w a 2 a 1 = 2 ∗ a 0 a 2 = a 0 Denominator\,Coefficients = \begin{cases} a0 = \frac{wa^2}{1+\sqrt(2)*wa+wa^2} \\ a1 = 2*a0 \\ a2 = a0\end{cases} De n o mina t or C oe ff i c i e n t s = ⎩ ⎨ ⎧ a 0 = 1 + ( 2 ) ∗ w a + w a 2 w a 2 a 1 = 2 ∗ a 0 a 2 = a 0 N u m e r a t o r C o e f f i c i e n t s = { b 0 = 1 b 1 = − 2 ( w a 2 − 1 ) 1 + ( 2 ) ∗ w a + w a 2 b 2 = − 1 + ( 2 ) ∗ w a − w a 2 1 + ( 2 ) ∗ w a + w a 2 Numerator\,Coefficients = \begin{cases} b0 = 1 \\ b1 = \frac{-2(wa^2-1)}{1+\sqrt(2)*wa+wa^2} \\ b2 = \frac{-1+ \sqrt(2)*wa-wa^2}{1+\sqrt(2)*wa+wa^2}\end{cases} N u m er a t or C oe ff i c i e n t s = ⎩ ⎨ ⎧ b 0 = 1 b 1 = 1 + ( 2 ) ∗ w a + w a 2 − 2 ( w a 2 − 1 ) b 2 = 1 + ( 2 ) ∗ w a + w a 2 − 1 + ( 2 ) ∗ w a − w a 2
Filter is applied both forward and backward (for minimal phase distortion) using filter coefficients (a0, a1, a2) and (b0, b1, b2) to compute the filtered signal
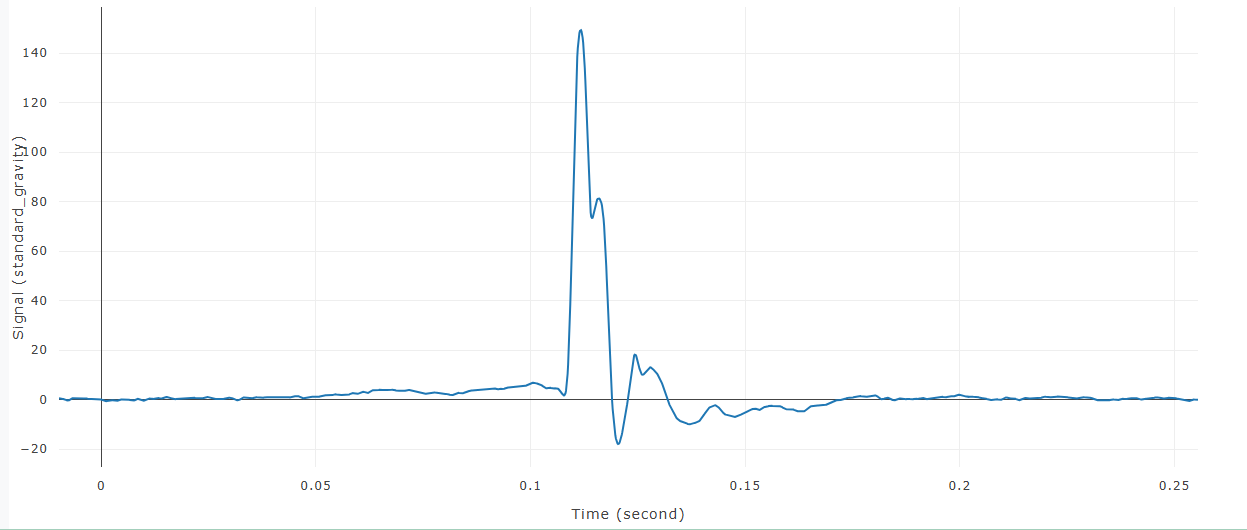
Butterworth Filter
Before Butterwoth Filter is applied to the signal
After Butterworth Filter is removed from signal